Spin magnetic moment
Contents |
Basis for spin magnetic moments
A spin magnetic moment is induced by all charged particles. The electron is an example of one such charged particle. A spin magnetic moment is created because a particle has physical properties known as spin and electric charge. The spin within classical physics would be an object that rotates axially around its center of mass. In quantum mechanics, elementary particles are points, which have no axis to revolve around. This means these particles do not have spin in a classical sense, as angular momentum is defined by 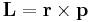 , but have the physical property of angular momentum (see Spin (physics)). Maxwell's theory of magnetic fields dictates that any moving charged particle creates a magnetic moment, and by definition, angular momentum designates movement. This is where the magnetic moment emerges in classical electromagnetism. See Maxwell's equation
, but have the physical property of angular momentum (see Spin (physics)). Maxwell's theory of magnetic fields dictates that any moving charged particle creates a magnetic moment, and by definition, angular momentum designates movement. This is where the magnetic moment emerges in classical electromagnetism. See Maxwell's equation
Calculation
We can calculate the observable spin magnetic moment (a vector), 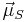 , for a sub-atomic particle with charge
, for a sub-atomic particle with charge  , mass
, mass  , and spin angular momentum (also a vector),
, and spin angular momentum (also a vector), 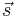 , via:
, via:
-
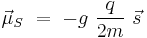
(
where  is a dimensionless number, called the g-factor. This number depends on the particle: it is
is a dimensionless number, called the g-factor. This number depends on the particle: it is 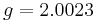 for the electron,
for the electron, 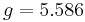 for the proton, and
for the proton, and 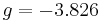 for the neutron. The proton and neutron are composed of quarks, which have a non-zero charge and a spin of
for the neutron. The proton and neutron are composed of quarks, which have a non-zero charge and a spin of 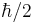 , and this must be taken into account when calculating their g-factors. Even though the neutron has a charge
, and this must be taken into account when calculating their g-factors. Even though the neutron has a charge 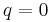 , its quarks give it a magnetic moment. The proton and electron's spin magnetic moments can be calculated by simply setting
, its quarks give it a magnetic moment. The proton and electron's spin magnetic moments can be calculated by simply setting 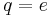 .
.
The intrinsic electron magnetic dipole moment is approximately equal to the Bohr magneton because 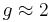 and the electron's spin is also
and the electron's spin is also 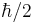 :
:
-
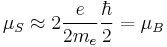
(
Eq. (2) is normally written as
-
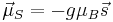
(
where μB is the Bohr magneton.
Just like the total spin angular momentum cannot be measured, neither can the total spin magnetic moment be measured. Equations (1) - (3) give the physical observable, that component of the magnetic moment measured along an axis, relative to or along the applied field direction. Conventionally, the z-axis is chosen but the observable values of the component of spin angular momentum along all three axes (assuming a Cartesian coordinate system) are each 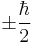 . However, in order to obtain the magnitude of the total spin angular momentum, wave mechanical corrections dictate that
. However, in order to obtain the magnitude of the total spin angular momentum, wave mechanical corrections dictate that  be replaced by its eigenvalue,
be replaced by its eigenvalue, 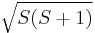 . In turn, calculation of the magnitude of the total spin magnetic moment requires that Eq. (3) be replaced by:
. In turn, calculation of the magnitude of the total spin magnetic moment requires that Eq. (3) be replaced by:
-
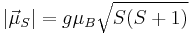
(
Thus, for a single electron, with spin quantum number 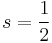 , the component of the magnetic moment along the field direction is, from Eq. (3),
, the component of the magnetic moment along the field direction is, from Eq. (3), 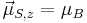 , or one BM, while the [magnitude of the] total spin magnetic moment is, from Eq. (4),
, or one BM, while the [magnitude of the] total spin magnetic moment is, from Eq. (4), 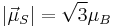 , or 1.73 BM.
, or 1.73 BM.
The analysis is readily extended to the spin-only magnetic moment of an atom. For example, the total spin magnetic moment (sometimes referred to as the effective magnetic moment when the orbital moment contribution to the total magnetic moment is neglected) of a transition metal ion with a single d electron outside of closed shells (e.g. Ti3+) is 1.73 μB since S = 1/2, while an atom with two unpaired electrons (e.g. V3+) with S = 1 would have an effective magnetic moment of 2.83 μB.
Spin in chemistry
Spin magnetic moments create a basis for one of the most important principles in chemistry, the Pauli exclusion principle. This principle, first suggested by Wolfgang Pauli, governs most of modern-day chemistry. The theory plays further roles than just the explanations of doublets within electromagnetic spectrum. This additional quantum number, spin, became the basis for the modern standard model used today, which includes the use of Hund's rules, and an explanation of beta decay.
History of spin magnetic moments
The idea of a spin angular momentum was first proposed in a 1925 publication by George Uhlenbeck and Samuel Goudsmit to explain hyperfine splitting in atomic spectra.[1] In 1928, Paul Dirac provided a rigorous theoretical foundation for the concept with his relativistic equation of motion for the wavefunction of the electron.[2]
Notes
- ^ Earlier the same year, Ralph Kronig discussed the idea with Wolfgang Pauli, but Pauli criticized the idea so severely that Kronig decided not to publish it.(Scerri 1995)
- ^ (Dirac 1928)
References
- Dirac, P. A. M. (1928-02-01). "The Quantum Theory of the Electron". Proceedings of the Royal Society of London: Series A 117 (778): 610–624. Bibcode 1928RSPSA.117..610D. doi:10.1098/rspa.1928.0023.
- Scerri, Eric R. (1995). "The exclusion principle, chemistry and hidden variables". Synthese 102 (1): 165–169. doi:10.1007/BF01063903.
External links
- An Introduction to the Electronic Structure of Atoms and Molecules by Dr. Richard F.W. Bader (McMaster University)